Sound will first disappear when sound waves originating from center and from either end of the slit are
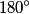 out of phase. This will occur when the path difference for waves originating from the center and from either end of the slit is out of phase. This will occur when the path difference for waves originating from the center and from either end of the slit is 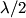 , where , where 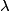 is the wavelength of the sound wave. This path difference will be is the wavelength of the sound wave. This path difference will be 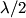 at an angle of at an angle of 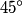 if the following condition is satisfied if the following condition is satisfied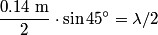 The relationship between 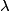 , the frequency , the frequency 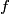 , and the speed of sound , and the speed of sound  , is , is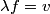 So, the condition for destructive interference at 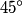 in terms of the frequency is in terms of the frequency is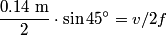 Plugging in 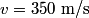 and solving for and solving for 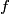 gives gives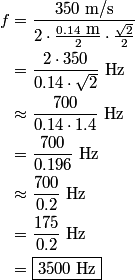 Therefore, answer (D) is correct. |